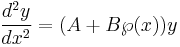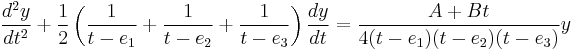Lamé function

In mathematics, a Lamé function (or ellipsoidal harmonic function) is a solution of Lamé's equation, a second-order ordinary differential equation. It was introduced in the paper (Gabriel Lamé 1837). Lamé's equation appears in the method of separation of variables applied to the Laplace equation in elliptic coordinates. In some special cases solutions can be expressed in terms of polynomials called Lamé polynomials.

Lamé functions are discussed in detail in (Arthur Erdélyi, Wilhelm Magnus & Fritz Oberhettinger et al. 1955, Chapter XV)

Lamé's equation is

$\frac{d^2y}{dx^2} = (A%2BB\weierp(x))y$

where A and B are constants, and 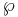$\wp$ is the Weierstrass elliptic function. The most important case is when B is of the form n(n + 1) for an integer n, in which case the solutions extend to meromorphic functions defined in the whole complex plane. For other values of B the solutions have branch points.

By changing the independent variable, Lamé's equation can also be rewritten in algebraic form as

$\frac{d^2y}{dt^2} %2B\frac{1}{2}\left(\frac{1}{t-e_1}%2B\frac{1}{t-e_2}%2B\frac{1}{t-e_3}\right)\frac{dy}{dt} = \frac{A%2BBt}{4(t-e_1)(t-e_2)(t-e_3)}y$

which after a change of variable becomes a special case of Heun's equation.

References

Erdélyi, Arthur; Magnus, Wilhelm; Oberhettinger, Fritz; Tricomi, Francesco G. (1955), Higher transcendental functions. Vol. III, McGraw-Hill Book Company, Inc., New York-Toronto-London, MR 0066496, http://apps.nrbook.com/bateman/Vol3.pdf
Lamé, G. (1837), "Sur les surfaces isothermes dans les corps homogènes en équilibre de température", J. Math. Pures Appl. 2: 147–188
Rozov, N.Kh. (2001), "Lamé equation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=L/l057400
Rozov, N.Kh. (2001), "Lamé function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=L/l057410
Volkmer, H. (2010), "Lamé function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/29